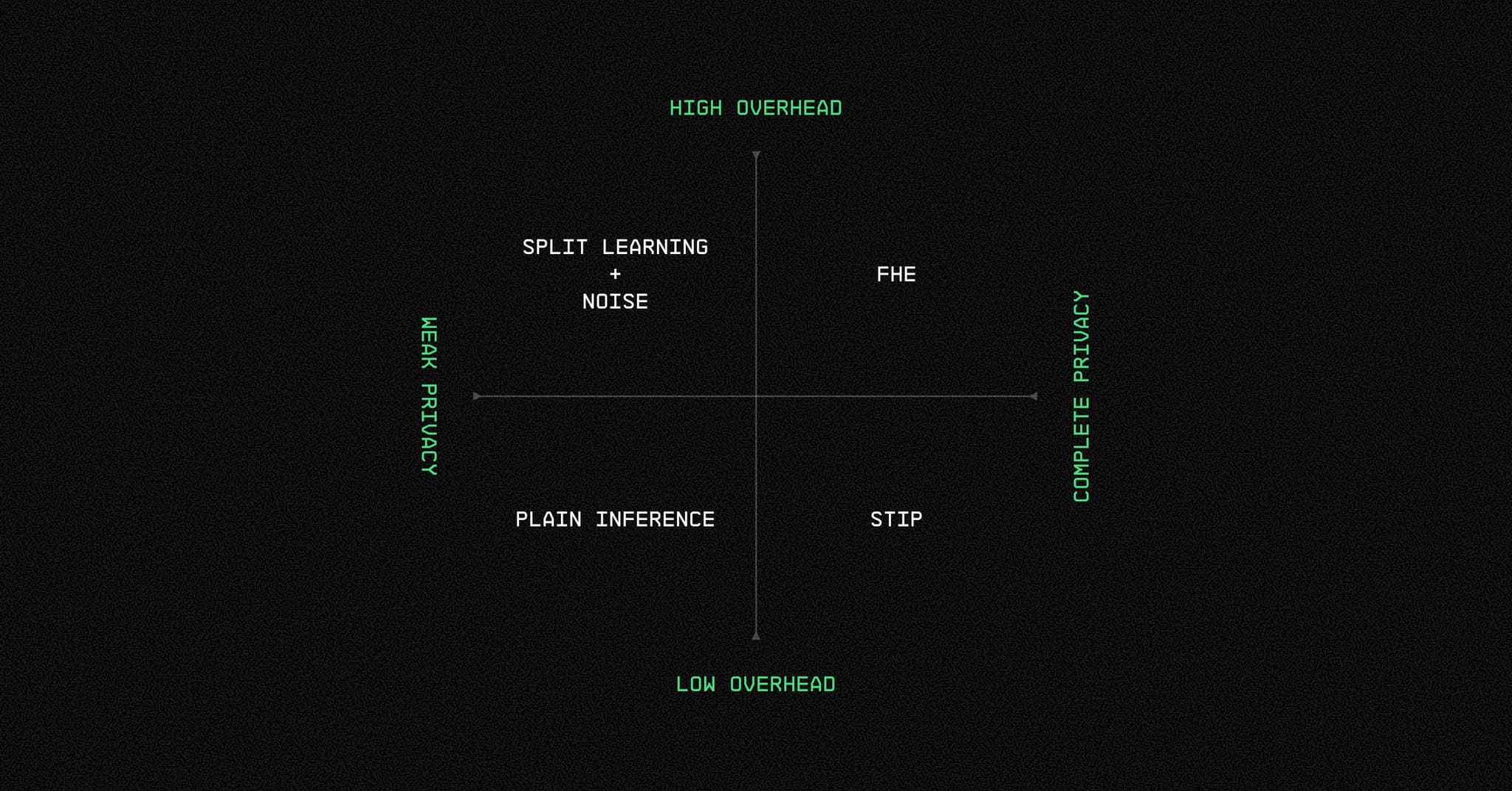
Hosting large models remotely presents risks in data privacy, as potentially sensitive inputs and outputs are exposed to unauthorized access. Protecting data privacy in LLM inference is thus critical.

However, this problem has been largely overlooked in the LLM space, as addressing it is complicated by constraints in efficiency and privacy-performance tradeoffs. Recent works on privacy-preserving model inference have primarily focused on cryptographic methods such as homomorphic encryption, introducing significant computational overhead that is unfeasible with scale (Liu & Liu, 2023).

Split-model approaches address efficiency by partitioning inference between local and remote compute to prevent raw inputs from ever leaving the user’s local device (Gupta & Raskar, 2018). Intermediate activations, however, contain information that make them vulnerable to input recovery attacks, limiting pure split-based data privacy (Shu et al., 2025).

To improve security, such approaches are often used in combination with perturbation methods such as privacy-preserving noise injection/censoring or adversarial split-learning (Chi et al., 2018; Samragh et al., 2020; Mai et al., 2023; Malekzadeh & Kawsar, 2024). These can often come at the cost of degrading performance, requiring additional training, and setting restrictions on compute allocation across devices.

To ensure trustworthy inference with LLMs at scale, particularly in the decentralized setting, we thus find it necessary to maintain model performance, robustly protect data privacy at both the input and output levels, be model and attack-agnostic, and optimize for compute efficiency flexibly to local and network capacities. We describe the Secure Transformer Inference Protocol (STIP, Yuan et al., 2024) for privacy-preserving LLM inference through an elegant mathematical property: carefully designed permutations that preserve computation while hiding data. Unlike heavyweight cryptographic approaches, STIP adds negligible overhead while providing practical privacy guarantees in real-world deployments.

Secure Transformer Inference Protocol

The key idea behind the effectiveness of STIP is to set up a three-party system, split the inference between two parties, and let the third actor generate permutations, thereby updating the weights of the model.

Three-party inference split

Inference is distributed across three entities:

• Model Developer: Holds the original model parameters and secret transformation keys.
• Model Server: Hosts only transformed parameters and executes inference on transformed activations.
• Data Owner: Encodes/decodes transformations to protect raw inputs/outputs.

This split secures raw data and model parameters to prevent privacy leakage and reflects real-world settings of model development and deployment.

Security Model

STIP operates under a three-party trust model where:

Data Owner: Holds permutation keys $(π, π_c)$ privately, never shares them model server

Model Server: Holds only transformed weights, never sees permutation keys

Model Developer: Generates and distributes keys/weights, then goes offline

The Model Server performing inference NEVER has access to the permutation matrices, making it impossible to recover raw inputs from permuted data.

Optimized for Transformer Architecture

STIP is specifically designed for the dominant architecture in LLMs - transformers. By focusing on linear operations and permutation-equivariant activations (ReLU, GELU, Softmax), STIP achieves:

• Zero accuracy loss
• Minimal computational overhead
• Provable security properties

Transformer Permutations

The logic of STIP masking is to permute all matrices in a semi-symmetrical way so they cancel each other out; input permutation is done on the client side and then reversed again at the client side in the end.

STIP Algorithm (Yuan et al., 2024)

We generate the following permutation matrices:

• $\pi$ is a permutation matrix in $\mathbb{R}^{n \times n}$ and will permute the input sequence $𝑥$.
• $\pi_c$ is a permutation matrix in $\mathbb{R}^{c \times c}$ and will permute the classifier $W_c$ as well as the output $o$.

For all 𝐿-layers we will generate the following permutation matrices:

• $\pi_{𝑖,1}$ will permute Query and Key matrices $W_q$ and $W_k$.
• $\pi_{𝑖,2}$ will permute Value and Output matrices $W_v$ and $W_o$.
• $\pi_{𝑖,3}$ will permute the weights in feed-forward sub-block $W_1$ and $W_2$ (Gated FFN).

The entire transformer function $𝑓(𝑥) = 𝑦$ is transformed into $f'(x\pi) = 𝑦'$ where $o' = o\pi_c^T$ . As such, when the client receives the output $o'$, it can re-permute it back to $o$ by multiplying with $\pi c$.

The permuted input embeddings $x\pi$ is transformed into three matrices $Q, K, V$ using learned & permuted weight matrices $W_q', W_k', W_v'$ ∈ $\mathbb{R}^{d \times d}$:

$$W_q' = \pi^T W_q \pi_{i,1} \quad\quad\quad W_k' = \pi^T W_k \pi_{i,1} \quad\quad\quad W_v' = \pi^T W_v \pi_{i,2} \\ Q = x W_q' \text{ for Query} \quad\quad K = x W_k' \text{ for Key} \quad\quad V = x W_v' \text{ for Value}$$

Notice how when the semi-symmetry of the permutation matrices allows us to cancel out the $\pi$ and $\pi^𝑇$ :

$$\begin{align}Q &= x(\pi\pi^T)W_q\pi_{i,1} = xW_q\pi_{i,1} \\K &= x(\pi\pi^T)W_k\pi_{i,1} = xW_k\pi_{i,1} \\V &= x(\pi\pi^T)W_v\pi_{i,2} = xW_v\pi_{i,2}\end{align}$$

and the right hand-side permutations will then be cancelled by the other semi-symmetrical permutation matrices in the end. Next comes $W' = \pi^T 𝑊 \pi$ which is multiplied with $V$ as:

$$VW_o' = xW_v(\pi_{i,2}\pi_{i,2}^T)W_o\pi = xW_vW_o\pi$$

and so on...

For layers without learnable parameters, STIP requires column-wise permutation equivariance, i.e., satisfying $f(x\pi) = f(x)\pi$ . Examples include ReLU, GeLU, SoftMax, and Sigmoid activations. STIP cannot be extended to convolutional or recurrent layers.

Permutation Rotation for Long-term Security

In decentralized settings where roles may change over time, we implement permutation rotation:

Scenario: A current Data Owner (who knows $π$) might later become a Model Server. Without rotation, they could potentially recover inputs from other users using the same π.

Solution: We implement a robust key rotation protocol:

1. Multi-key approach: Prevent the user to become a server. In a permissionless setting this is not possible. However, what we can do is to make it really hard for the user to become a server! One way of doing this is to compute several permutations of all weights and randomly choose one set of permutations for each forward pass. This way, even if the user knows 𝜋, it may not receive an embedding permuted with that same 𝜋 when it becomes a server.
2. Periodic rotation: Rotate the permutation. While option (1) is a measure in it self, it is probabilistic and will fail as the server handles numerous forward passes. What we can do is to rotate the permutation matrix 𝜋 and have all servers update their local already-permuted weights again.

Periodic permutation rotation ensures past permutation knowledge provides no advantage, maintaining security even in dynamic, permissionless networks.

Re-permuting an already permuted weight $W$ with a new permutation $\pi'$ is efficient and does not expose the underlying weight. Only the input and output permutations ( $\pi$ and $\pi_c$ ) need refreshing; not the internal permutations ( $\pi_{i,1}$, $\pi_{i,2}$, $\pi_{i,3}$ ). This is achieved by sending a semi-symmetrical matrix for each weight, which cancels out the previous permutation $\pi$ and applies the new $\pi'$ .

Threat Model and Assumptions

STIP with rotations protects against:

• Honest-but-curious Model Servers attempting to read user inputs/outputs
• External observers of network traffic
• Attempts to recover original model weights

Assumes:

• Model Developer is trusted during initial setup
• Data Owners keep permutation keys private
• Regular key rotation in decentralized settings

Future Work

STIP demonstrates that practical privacy-preserving LLM inference is achievable without sacrificing performance or accuracy. By leveraging the mathematical properties of transformers and a carefully designed three-party protocol, STIP provides:

• Real-world deployability with minimal overhead
• Provable privacy against realistic threat models
• Perfect accuracy preservation through algebraic cancellation
• Flexible deployment in decentralized settings

Building on this foundation, our next focus is developing multi-party permutation generation protocols. This advancement would eliminate the current requirement for data owners to exclusively hold permutation keys, instead enabling distributed key generation where no single party possesses complete permutation information.

Such a protocol would:

• Enable trustless collaboration between data owners and inference providers
• Remove single points of failure in key management
• Support fully decentralized inference networks where trust assumptions are minimized

This evolution represents the natural progression toward fully trustless, privacy-preserving LLM inference infrastructure.

References

1. Chi, L., Jiang, B., & Mu, Y. (2018). Fast Fourier Transform-based Scalable Secure Aggregation for Privacy-Preserving Federated Learning. arXiv preprint arXiv:1812.02863. https://arxiv.org/abs/1812.02863
2. Gupta, O., & Raskar, R. (2018). Distributed learning of deep neural network over multiple agents. Journal of Network and Computer Applications. https://arxiv.org/abs/1810.06060
3. Liu, T., & Liu, Y. (2023). Homomorphic Encryption for Large Language Model Inference. arXiv preprint arXiv:2305.18396. https://arxiv.org/abs/2305.18396
4. Mai, G., et al. (2023). Split Learning with Differential Privacy for Large Language Models. arXiv preprint arXiv:2310.09130. https://arxiv.org/abs/2310.09130
5. Malekzadeh, M., & Kawsar, F. (2024). Privacy-Preserving Split Learning with Adversarial Perturbations. arXiv preprint arXiv:2310.13384. https://arxiv.org/abs/2310.13384
6. Samragh, M., et al. (2020). Privacy-Preserving Deep Learning via Weight Transmission. OpenReview. https://openreview.net/forum?id=iqmOTi9J7E8
7. Shu, R., et al. (2025). On the Privacy of Split Learning. arXiv preprint arXiv:2501.05965. https://arxiv.org/abs/2501.05965
8. Yuan, Z., et al. (2024). Secure Transformer Inference Protocol. arXiv preprint arXiv:2312.00025. https://arxiv.org/abs/2312.00025